Selected research highlights:
Minimal pole representation for spectral functions
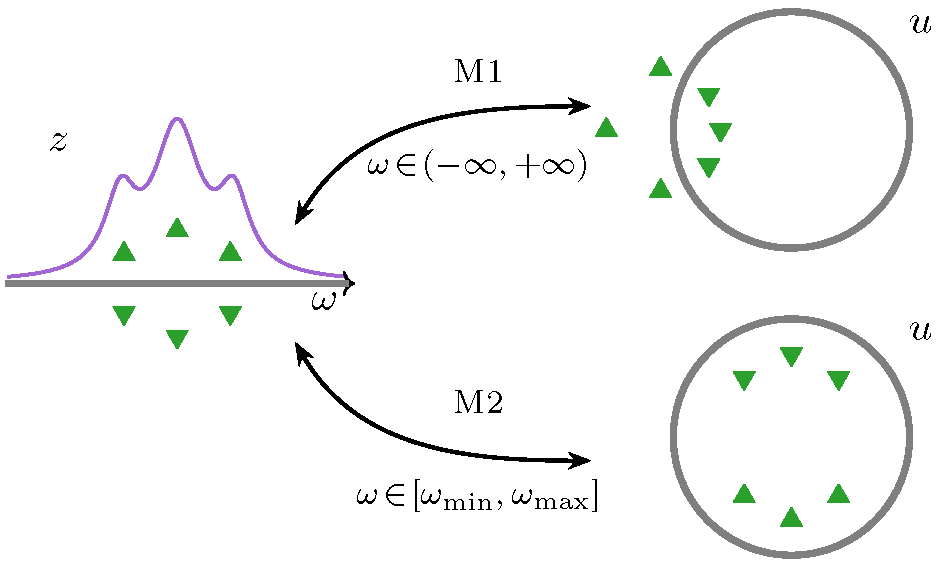
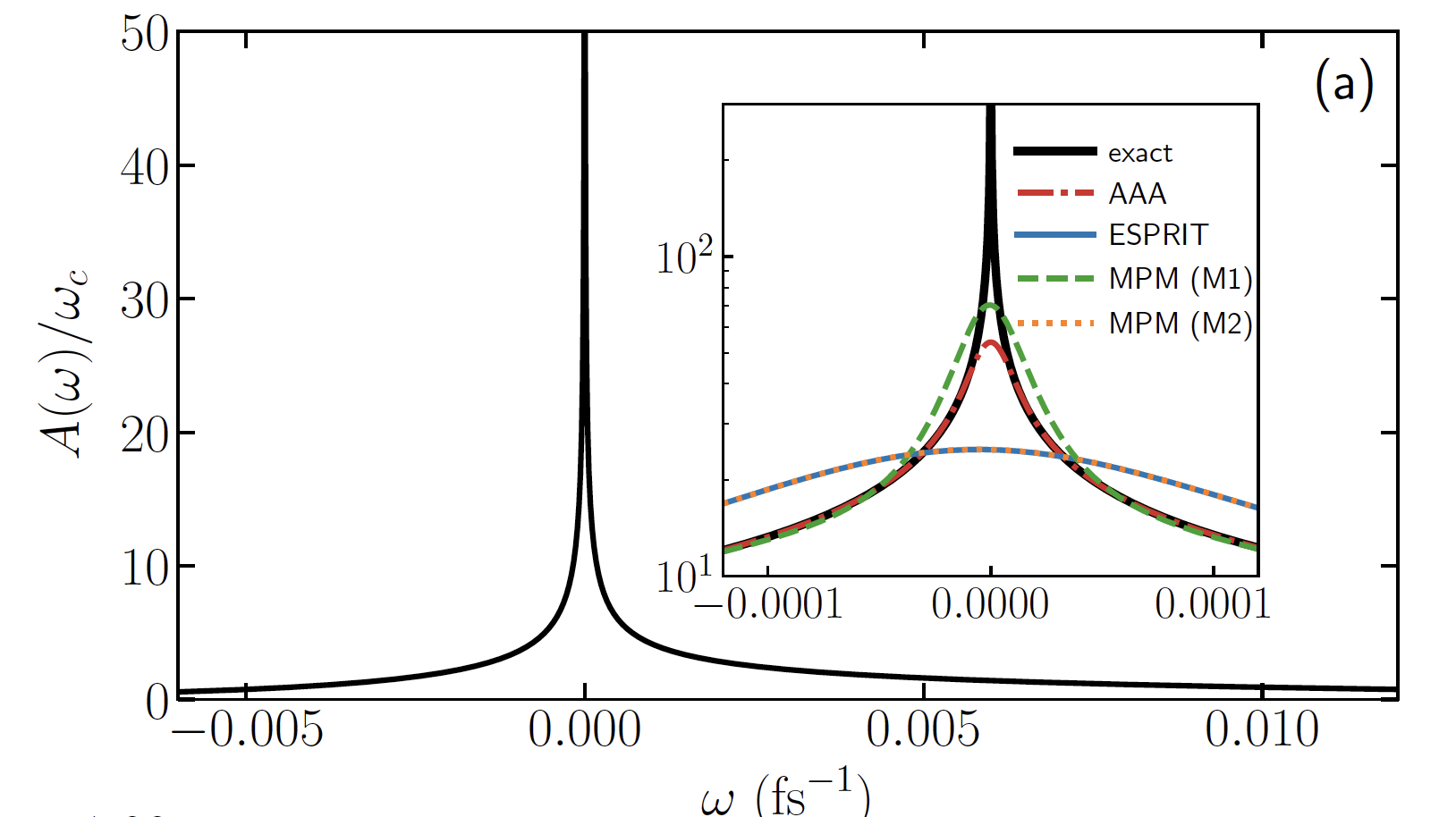
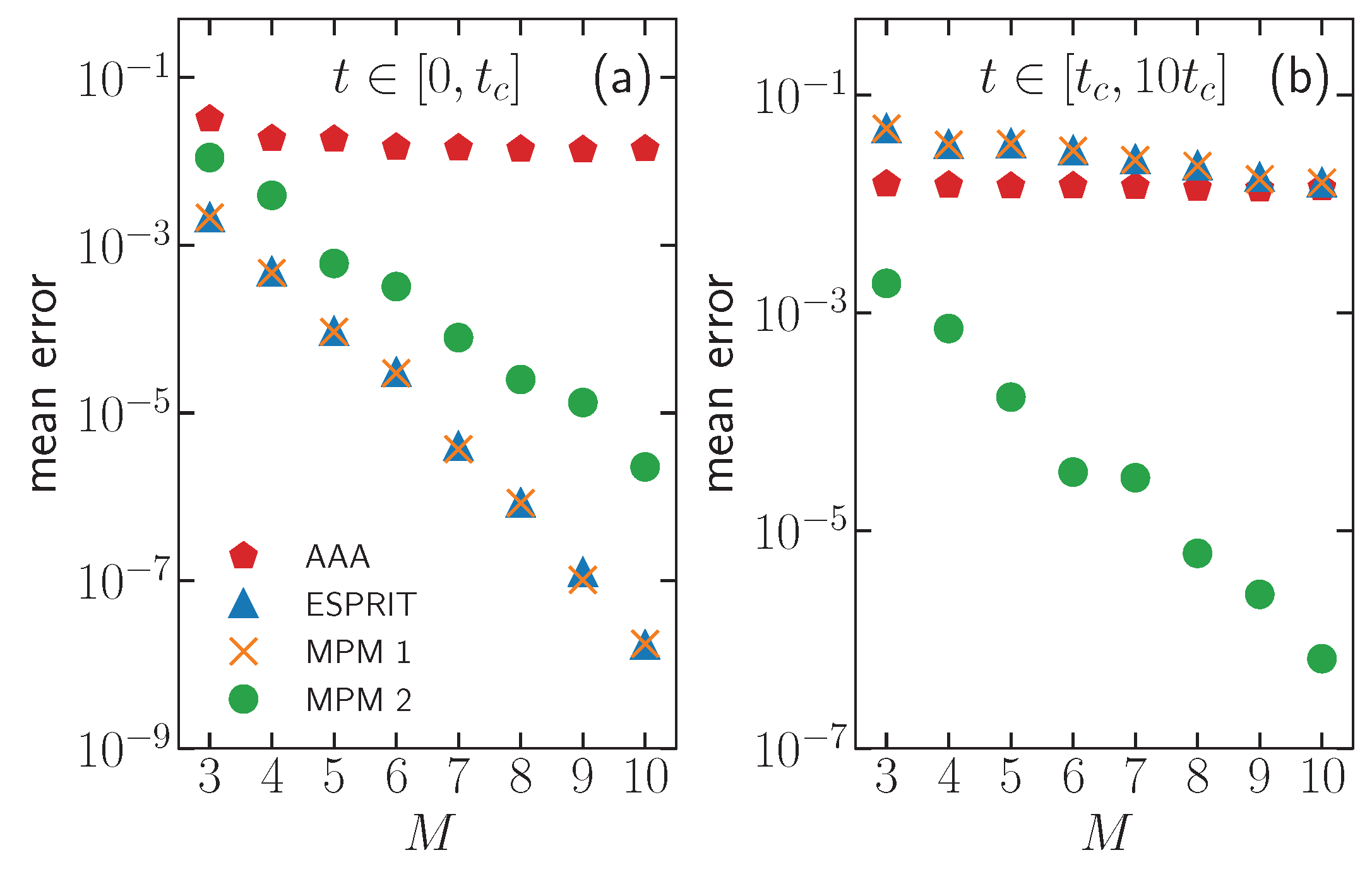
Representing spectral densities, real-frequency, and real-time Green’s functions of continuous systems by a small discrete set of complex poles is a ubiquitous problem in condensed matter physics, with applications ranging from quantum transport simulations to the simulation of strongly correlated electron systems. This paper introduces a method for obtaining a compact, approximate representation of these functions, based on their parameterization on the real axis and a given approximate precision. We show applications to typical spectral functions and results for structured and unstructured correlation functions of model systems.
Recommended citation: Lei Zhang, André Erpenbeck, Yang Yu & Emanuel Gull, J. Chem. Phys. 162, 214111 (2025) [link].
Controlled analytic continuation of Matsubara correlation functions using minimal information principle
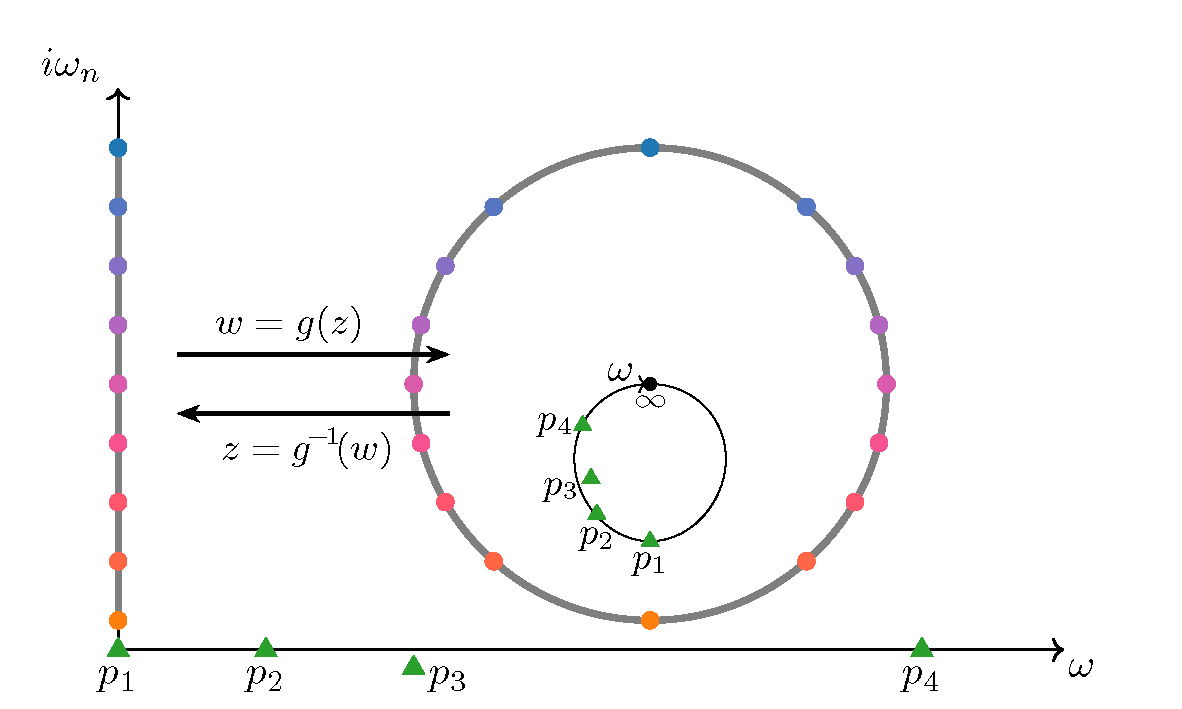
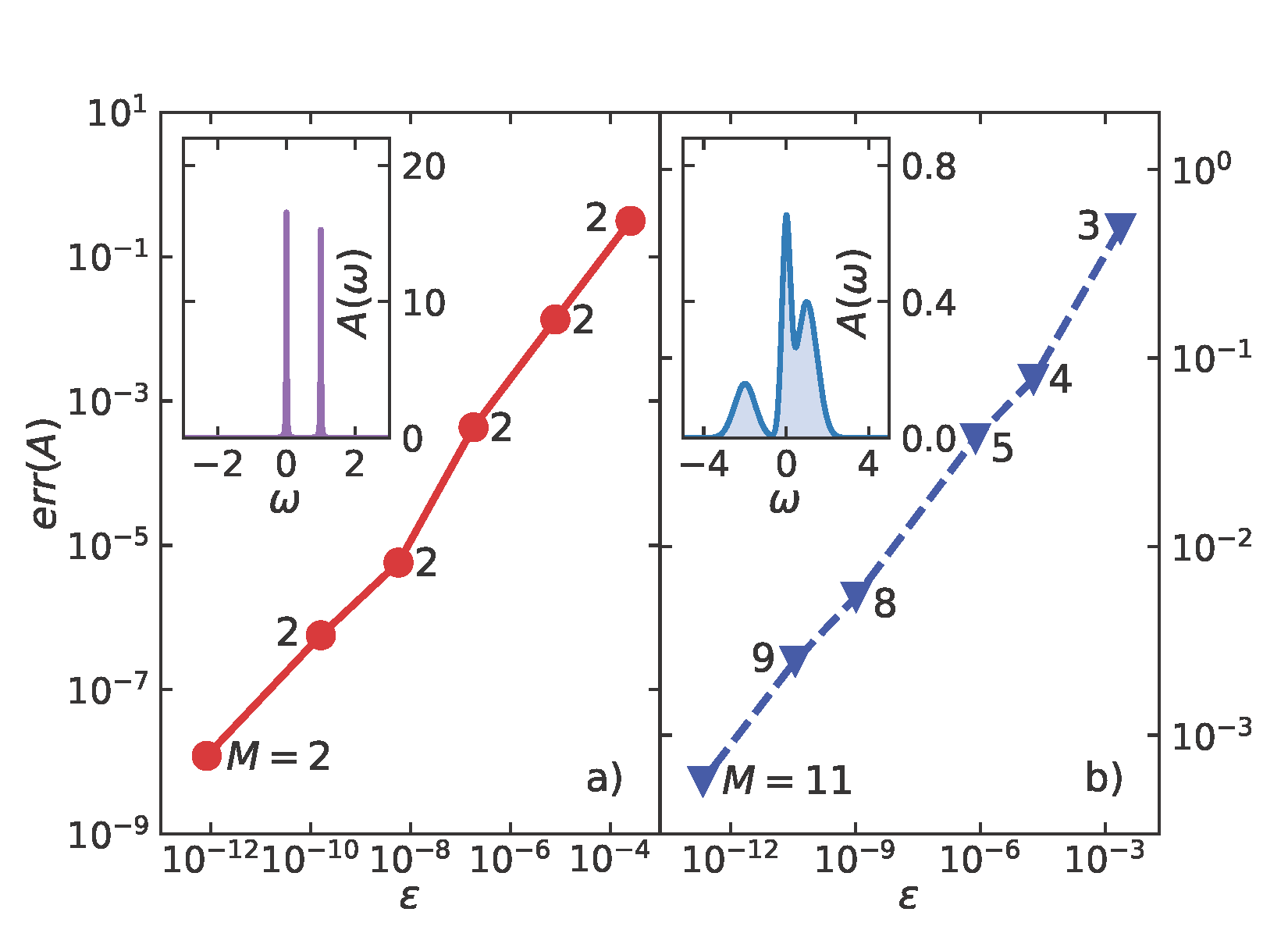
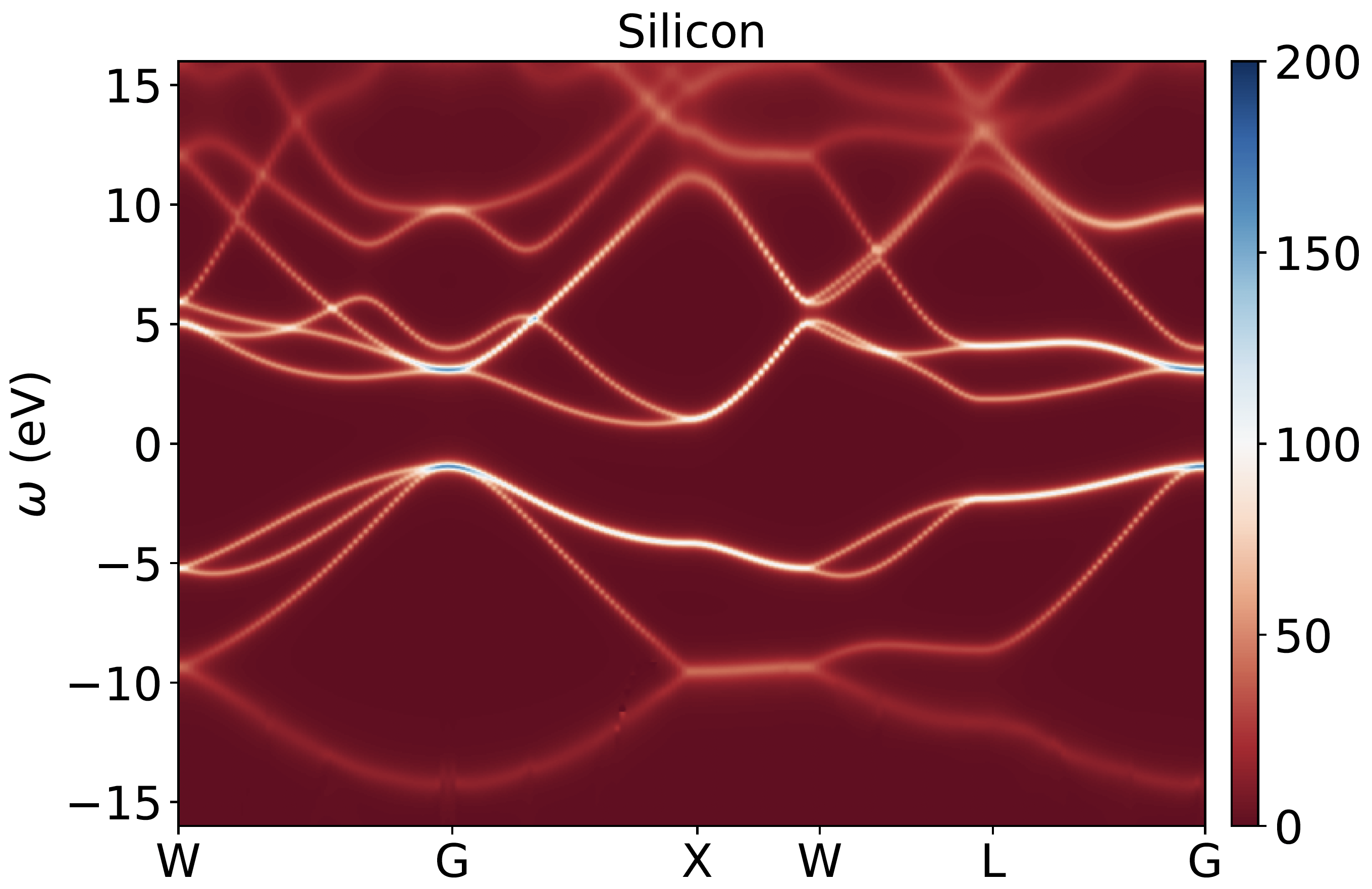
Analytic continuation is a crucial step in the simulation of finite-temperature field theories, where numerically obtained Matsubara data is extended to the real frequency axis for physical interpretation. However, numerical analytic continuation is an ill-posed problem, as uncertainties in the Matsubara axis are exponentially amplified. In this work, we introduce a systematic and controlled approach that approximates any Matsubara function—whether scalar- or matrix-valued—using a minimal pole representation within a predefined precision. We demonstrate systematic convergence to the exact spectral function on the real axis as a function of our control parameter across various physically relevant scenarios. Additionally, we compare results for real material systems against state-of-the-art methodologies. Our approach is robust against noise, offering a reliable path for analytic continuation in many-body theory, while providing direct access to the analytic structure of functions for deeper theoretical interpretation of physical properties.
Recommended citation: 1. Original paper: Lei Zhang & Emanuel Gull, Phys. Rev. B 110, 035154 (2024) [link]. 2. Technical details and matrix-valued generalization: Lei Zhang, Yang Yu & Emanuel Gull, Phys. Rev. B 110, 235131 (2024) [link] [Editors’ Suggestion].
Loop-Cluster Coupling and Algorithm for Classical Statistical Models
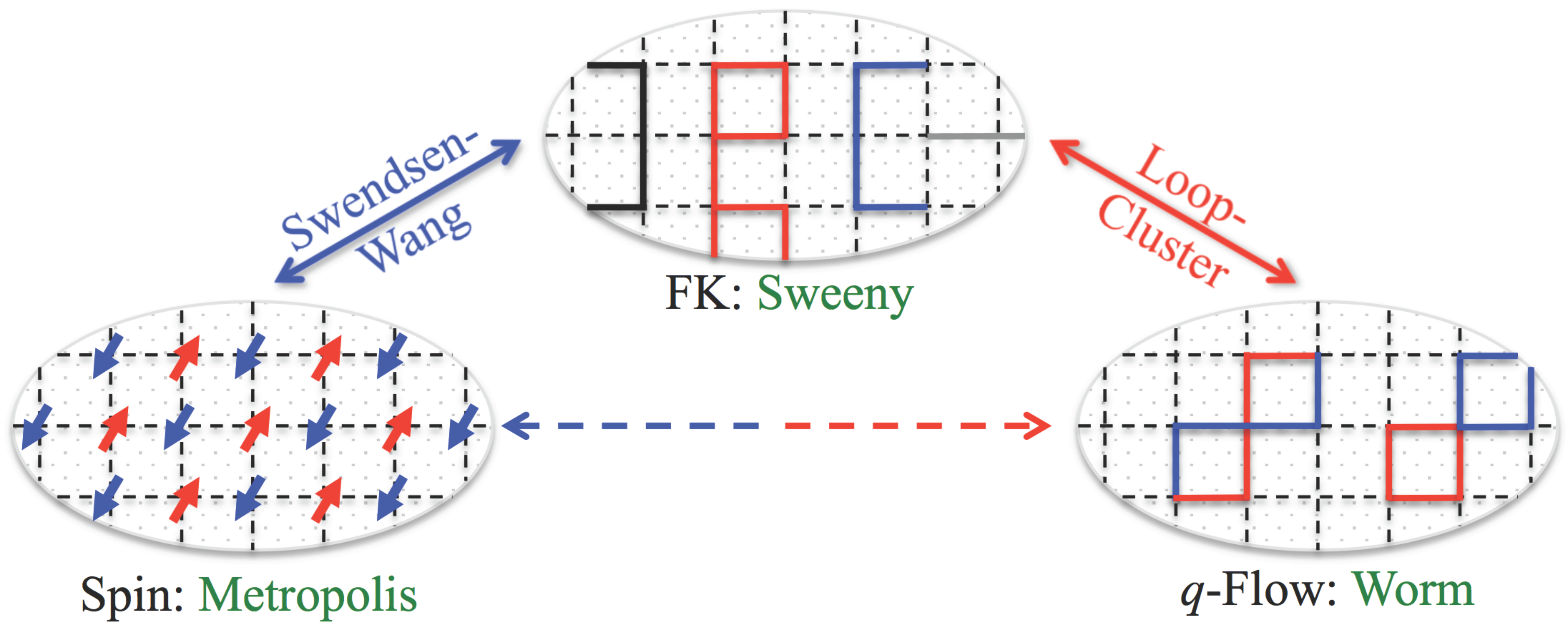
Potts spin systems play a fundamental role in statistical mechanics and quantum field theory, and can be studied within the spin, the Fortuin-Kasteleyn (FK) bond or the \(q\)-flow (loop) representation. We introduce a Loop-Cluster (LC) joint model of bond-occupation variables interacting with \(q\)-flow variables, and formulate a LC algorithm that is found to be in the same dynamical universality as the celebrated Swendsen-Wang algorithm. This leads to a theoretical unification for all the representations, and numerically, one can apply the most efficient algorithm in one representation and measure physical quantities in others. Moreover, by using the LC scheme, we construct a hierarchy of geometric objects that contain as special cases the \(q\)-flow clusters and the backbone of FK clusters, the exact values of whose fractal dimensions in two dimensions remain as an open question. Our work not only provides a unified framework and an efficient algorithm for the Potts model, but also brings new insights into rich geometric structures of the FK clusters.
Recommended citation: Lei Zhang, Manon Michel, Eren M. Elçi & Youjin Deng, Phys. Rev. Lett. 125, 200603 (2020) [link].
Graphical Representations and Worm Algorithms for the O(\(N\)) Spin Model

We present a family of graphical representations for the O(\(N\)) spin model, where \(N ≥ 1\) represents the spin dimension, and \(N =\) 1, 2, 3 corresponds to the Ising, \(XY\) and Heisenberg models, respectively. With an integer parameter \(0 \leq \ell \leq N/2\), each configuration is the coupling of \(\ell\) copies of subgraphs consisting of directed flows and \(N − 2\ell\) copies of subgraphs constructed by undirected loops, which we call the \(XY\) and Ising subgraphs, respectively. On each lattice site, the \(XY\) subgraphs satisfy the Kirchhoff flow-conservation law and the Ising subgraphs obey the Eulerian bond condition. Then, we formulate worm-type algorithms and simulate the O(\(N\)) model on the simplecubic lattice for \(N\) from 2 to 6 at all possible \(\ell\). It is observed that the worm algorithm has much higher efficiency than the Metropolis method, and, for a given \(N\), the efficiency is an increasing function of \(\ell\). Beside Monte Carlo simulations, we expect that these graphical representations would provide a convenient basis for the study of the O(\(N\)) spin model by other state-of-the-art methods like the tensor network renormalization.
Recommended citation: Longxiang Liu*, Lei Zhang*, Xiaojun Tan & Youjin Deng, Commun. Theor. Phys. 75, 115702 (2023) [link] [*: equal contribution].
